J. E. Villarino.- Desgraciadamente, es el tema de más actualidad. Pero casi siempre tratado desde una vertiente política partidista y poco científica. Me interesa que los lectores de Zonaretiro puedan disponer de algunos datos de cómo se comporta este virus altamente letal hoy por hoy y qué características lo diferencian de otras enfermedades infecciosas más conocidas.
Miles de personas han fallecido desde el mes de marzo de este año en los países del África occidental, y muchos más están cayendo enfermos todos los días, como recogen todos los medios de comunicación del mundo.
La epidemiología matemática se encarga de crear complejos modelos matemáticos y probabilísticos que intentan responder a tres preguntas clave acerca de los brotes: ¿Cuán contagiosas son estas enfermedades infecciosas? ¿Con qué rapidez se propagan? ¿Y cuánta gente va a fallecer por su causa? Estos modelos ayudan a los especialistas en Salud Pública de las instituciones y organismos nacionales y supranacionales a desarrollar estrategias para atacar los brotes específicos que periódicamente se suscitan.
Cómo se comportan las principales enfermedades infecciosas
Las enfermedades rara vez se comportan de igual manera a lo largo de los distintos brotes en que se manifiestan, dependiendo de múltiples factores tales como tipologías poblacionales, su grado de desarrollo, niveles sanitarios, hábitos culturales y un largo etcétera. Un brote puede propagarse más rápidamente o matar a un porcentaje mayor de personas que otro. Así que los datos se refieren a diferentes escenarios y se expresan en rangos.
Los datos que hoy traemos a nuestros lectores nos los brinda el epidemiólogo matemático Gerard Chowell de la Universidad Estatal de Arizona, que recoge el diario The Washington Post. Cada muestra de 100 aperturas con un ‘paciente 0’, la primera persona que se enferma.
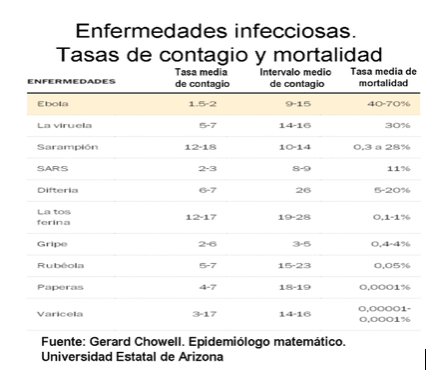
La tasa promedio de contagio es una medida de la facilidad con que una enfermedad viaja de persona a persona. Una tasa de 5 significa que cada persona enferma pasa la enfermedad a un promedio de cinco personas. Cuando el número es inferior a 1, la epidemia se extingue.
El intervalo promedio de contagio es el tiempo entre el primer paciente que muestra los síntomas y un caso secundario mostrando síntomas. Cuanto más, mejor, porque eso permite tiempo para encontrar y aislar a las personas que han estado expuestas antes de que se propaguen el virus.
Conocer la tasa de mortalidad ayuda a establecer prioridades, a partir de la asignación de dinero para luchar contra la enfermedad para decidir a quién vacunar. Si una enfermedad mata a más niños o personas mayores, por ejemplo, pueden obtener prioridad si los suministros de vacunas son limitadas. Cuando una vacuna contra el Ébola está listo, trabajadores de la salud probablemente recibirán las primeras dosis.
ElÉbola se propaga más lentamente, pero mata más que otras enfermedades infecciosas y afortunadamente, es más difícil de contraer
Según estos datos, se puede decir que en comparación con otras enfermedades infecciosas, el Ébola se propaga más lentamente que otros virus y afecta relativamente a menos personas. Pero es extremadamente mortal.
En cuanto a la tasa de mortalidad, es extremadamente alta con valores entre el 40%-70% respecto de las personas infectadas. Le siguen en orden de letalidad la viruela, el sarampión, el SARS y la difteria, con valores bastante más reducidos. A años luz, con mortalidad todavía mucho más bajas, figuran enfermedades comunes como la tos ferina, la gripe, la rubeola, las paperas y la varicela.
De las 10 enfermedades infecciosas de la tabla anterior, el Ébola tiene la tasa de contagio más baja con valores de 1,5 a 2,0, mientras que otras, mucho más leves, son sin embargo mucho más contagiosas con tasas de 12,0 a 18,0.
Ébola, el SARS y la varicela presentan más o menos la misma cantidad de tiempo para pasar de una persona enferma al siguiente grupo de personas, llamado ‘generación’. Si el Ébola fuera tan fácil de ser adquirido como la varicela, se contarían por miles las personas que habrían enfermado en la cuarta generación.
Simulación de un brote
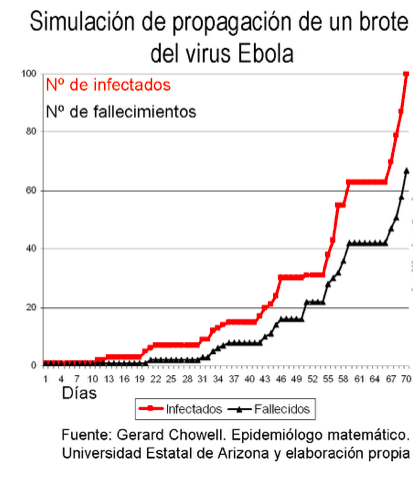
Partiendo del ‘paciente 0’ infectado, el gráfico representa una simulación realizada por el investigador de la propagación de la enfermedad hasta un total de 100 personas infectadas.
El eje de abscisas representa días. Como se ve en la simulación, se tardan 70 días en infectarse 100 individuos, de los que 67 cursaron en fallecimientos.
Como se observa, la curva responde a una tipología de curva exponencial es decir, de rápido crecimiento, y no presenta un perfil continuo sino en escalones, tanto en la evolución de los individuos infectados como en los fallecidos, de forma casi paralela, con una salvedad. El ‘gap’ o distancia entre ambos perfiles se agranda conforme se van infectando más individuos y la tasa de mortalidad relativa y absoluta aumenta.
Las curvas evidencian también que cuanto antes se controle la propagación y se establezcan eficaces controles sobre la población infectada, menor será la mortalidad en estos primeros estadios de la epidemia y mayores serán las posibilidades de control de la misma. Podemos decir que la dificultad de control de la epidemia crece exponencialmente conforme ésta avanza.
Los expertos no pintan nada, la ignorancia y prepotencia de los políticos lo ocupa todo
Todo apunta a que, de principio a fin, se ha producido una cadena de despropósitos: improvisación, instalaciones inadecuadas, personal sin la adecuada formación y entrenamiento, incumplimiento de los estándares y protocolos más avanzados, descoordinación entre administraciones que pone de manifiesto la necesidad de que la sanidad vuelva a la competencia estatal, reacciones tardías, falta de información, etc
Compartimos lo que dijo el profesor Javier M. Buldú el 9 octubre, 2014 en el blog científico MI+D “en este país también tenemos a algunos de los mayores expertos mundiales sobre propagación de enfermedades”.
Por nombrar a un par, Romulado Pastor-Satorras, físico al igual que el profesor Vespignani e investigador de la Universidad Politécnica de Cataluña. El profesor Pastor-Satorras ha publicado recientemente un artículo de revisión sobre los modelos matemáticos que permiten prever la transmisión de enfermedades en la sociedad.
Otro investigador residente en España desde hace más de 10 años es el Dr. Yamir Moreno, del Insitituto Universitario de Investigación en Biocomputación y Sistemas Complejos (Zaragoza). El Dr. Moreno ha destacado por sus innumerables aportaciones al campo del modelado de enfermedades y su relación con la estructura de la red social sobre la que se propagan, lo que le ha valido más de 12.000 citas, según Scholar Google. Vamos, que impacto desde luego ha tenido.
Y me dejo muchos más físicos por nombrar, que no están en Estados Unidos, ni en Alemania. Están aquí, en nuestras universidades y centros de investigación (a pesar de la que está cayendo). Estos investigadores saben cómo se propagan las enfermedades. Pueden estimar los riesgos, los tiempos de propagación, el número de personas infectadas, etc…
Y yo me pregunto, ¿por qué no vemos a ninguno de ellos en los medios de comunicación? ¿Ha contactado el gobierno con el profesor Pastor-Satorras o el Dr. Moreno? ¿Están en el gabinete de crisis sobre el ébola?
Puede que me equivoque, pero viendo como se está actuando, mucho me temo que conozco las respuestas…